OckBench: Tokens are Not to Be Multiplied without Necessity | NeurIPS 2025 Workshop on Efficient Reasoning

Introduction

"Entities must not be multiplied beyond necessity." — The Principle of Ockham's Razor

Large Language Models (LLMs) such as GPT-4, Claude 3, and Gemini have demonstrated remarkable capabilities in complex problem-solving, largely attributed to their advanced reasoning abilities. Techniques like Chain of Thought (CoT) prompting and self-reflection have become central to this success, enabling models to perform step-by-step deductions for tasks requiring deep knowledge and logical rigor. However, as the industry increasingly emphasizes this "long decoding" mode, the computational cost associated with these reasoning processes has grown significantly.

While LLM evaluation and comparison have become increasingly important, most evaluations focus primarily on accuracy while the efficiency of generation is less discussed. For example, HELM, LM-Eval, and the LMSYS Chatbot Arena rank models almost entirely on task accuracy. Yet in real systems, the difference between generating 10K tokens vs 100K tokens is non-trivial in latency, cost, and energy.

We introduce OckBench, the first model-agnostic, hardware-agnostic benchmark that jointly measures accuracy and decoding token count for reasoning and coding tasks. Our key contributions include:

Model-Agnostic Efficiency Metric: We formalize decoding token count as an intrinsic, hardware- and system-independent efficiency metric
Efficiency-Accuracy Aware Benchmark: The first unified benchmark specifically designed to evaluate LLM reasoning efficiency by measuring token consumption alongside accuracy
Empirical Trade-offs: We conduct experiments across multiple open- and closed-source models, revealing substantial practical trade-offs on the accuracy–efficiency Pareto frontier

Through experiments comparing multiple open- and closed-source models, we uncover that many models with comparable accuracy differ wildly in token consumption. For instance, among commercial models, one high-accuracy model required over 2× the tokens of another to achieve similar accuracy. This reveals that efficiency variance is a neglected but significant axis of differentiation in LLM evaluation.

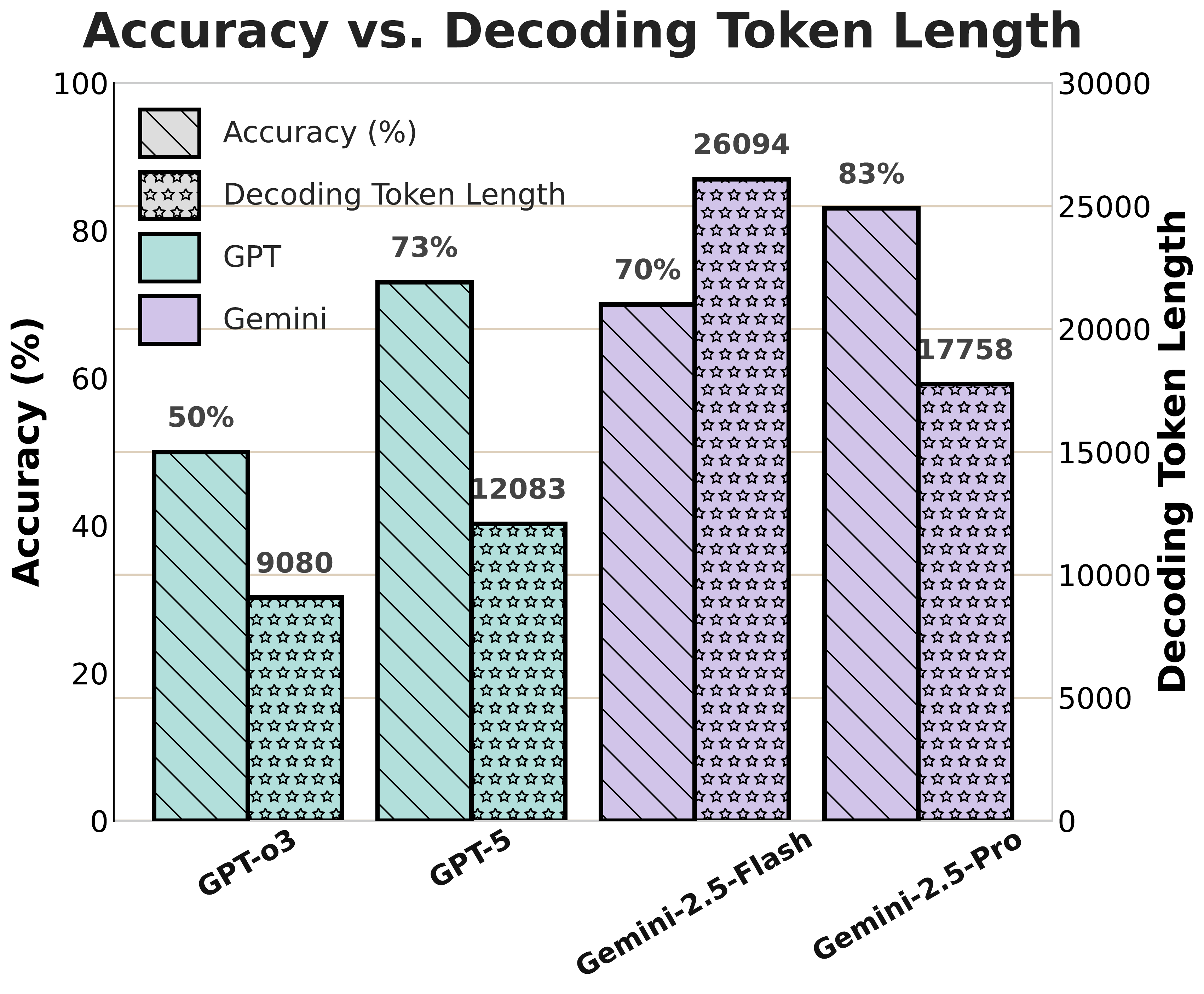
Model Performance Comparison across all evaluated models showing accuracy vs token efficiency trade-offs — Commercial models with similar performance level but spent token budget differently

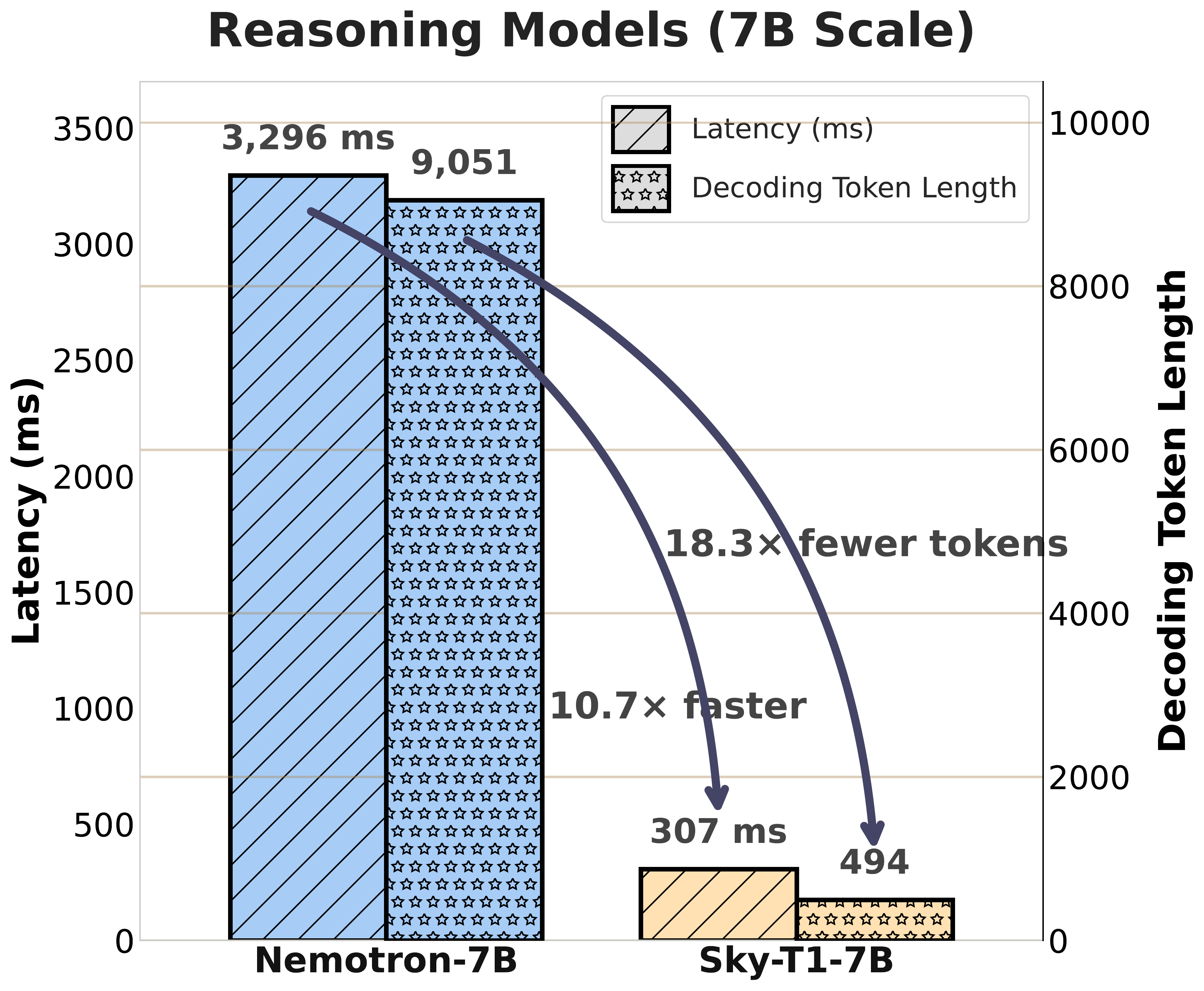
Performance comparison of 7B parameter models highlighting efficiency differences — Similar model size but takes drastically different time in reasoning tasks

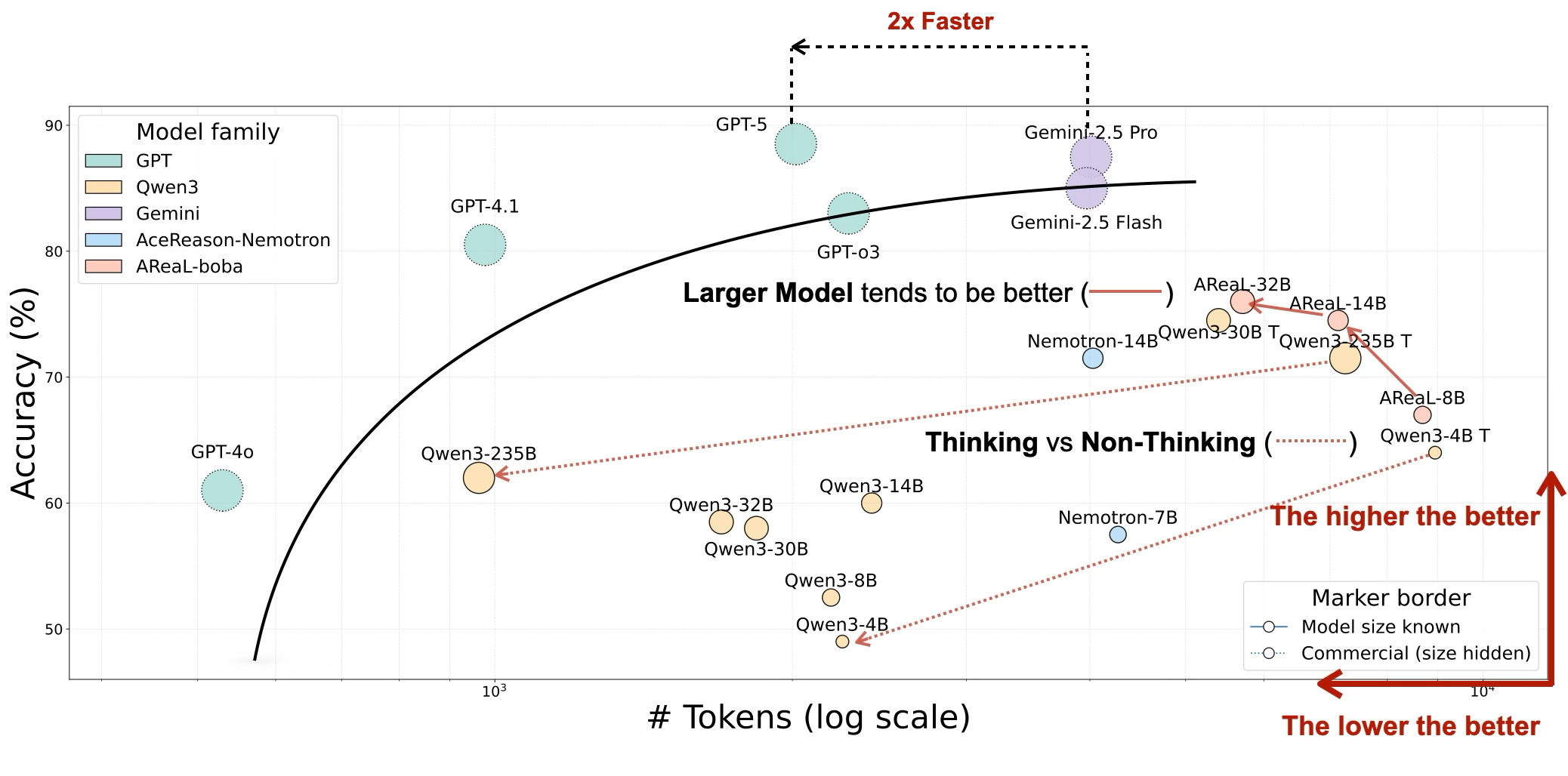
Accuracy vs token consumption trade-off analysis across dense and refined reasoning models — Accuracy vs. token consumption trade-off analysis across dense and refined reasoning models, demonstrating the efficiency frontier for different model configurations

Leaderboard

Performance of various LLMs on OckBench. Models are ranked by their reasoning efficiency, which is computed as #Tokens / Accuracy (lower is better). Click on the tabs to switch between Math and Coding domains.

OckBench-Math
OckBench-Coding

#	Model	Category	#Tokens	Accuracy (%)	Reasoning Efficiency
2	GPT-4.1 OpenAI	Commercial	1,349.88	59.00	152.1
3	Qwen3-30B-A3B (thinking) Alibaba	Open Source	4,139.33	83.00	138.1
4	GPT-5 OpenAI	Commercial	3,641.89	78.00	130.3
5	Qwen3-235B-A22B (thinking) Alibaba	Open Source	4,774.40	81.50	113.4
6	Gemini-3 Pro Google	Commercial	6,190.85	88.00	110.1
7	GPT-4o OpenAI	Commercial	570.17	38.50	100.1
8	Qwen3-14B (thinking) Alibaba	Open Source	5,084.48	79.00	97.0
9	GPT-o3 OpenAI	Commercial	3,513.90	69.50	95.5
10	Qwen3-32B (thinking) Alibaba	Open Source	4,797.89	76.50	93.3
11	Gemini-2.5 Pro Google	Commercial	6,392.96	83.00	89.4
12	AReaL-boba-2-32B inclusionAI	Open Source	5,387.96	78.00	88.1
13	AReal-boba-2-14B inclusionAI	Open Source	6,154.75	79.50	81.6
14	Qwen3-8B (thinking) Alibaba	Open Source	6,302.89	80.00	81.2
15	AReal-boba-2-8B inclusionAI	Open Source	7,026.88	79.00	70.2
16	Qwen3-4B (thinking) Alibaba	Open Source	6,478.45	72.00	57.6
17	Gemini-2.5 Flash Google	Commercial	7,984.58	74.50	51.8
18	AceReason-Nemotron-7B NVIDIA	Open Source	4,022.79	57.00	46.0
19	AceReason-Nemotron-14B NVIDIA	Open Source	4,147.26	56.50	43.5
20	Qwen3-235B-A22B (non-thinking) Alibaba	Open Source	980.29	34.50	41.9
21	Qwen3-14B (non-thinking) Alibaba	Open Source	2,421.85	43.50	34.0
22	Qwen3-32B (non-thinking) Alibaba	Open Source	1,713.91	36.00	27.2
24	Qwen3-8B (non-thinking) Alibaba	Open Source	2,081.88	29.00	11.7
25	Qwen3-4B (non-thinking) Alibaba	Open Source	2,262.83	27.50	9.2
26	Qwen3-30B-A3B (non-thinking) Alibaba	Open Source	1,852.56	25.00	8.4

#	Model	Category	#Tokens	Accuracy (%)	Reasoning Efficiency
1	Qwen3-235B-A22B (non-thinking) Alibaba	Open-Source	519.31	61.00	851.3
2	gpt-4.1 OpenAI	Commercial	639.80	74.50	858.1
3	Qwen3-32B (non-thinking) Alibaba	Open-Source	493.23	53.50	921.9
4	gpt-4o OpenAI	Commercial	573.54	61.50	932.6
5	Qwen3-30B-A3B (non-thinking) Alibaba	Open-Source	631.42	54.00	1,169.3
6	gpt-5 OpenAI	Commercial	1,584.41	96.50	1,641.8
7	Qwen3-14B (non-thinking) Alibaba	Open-Source	990.27	51.00	1,941.7
8	Qwen/Qwen3-4B Alibaba	Open-Source	893.80	39.50	2,263.8
9	Qwen3-4B (non-thinking) Alibaba	Open-Source	893.80	39.50	2,263.8
10	o3 OpenAI	Commercial	2,335.24	93.50	2,497.6
11	Qwen3-8B (non-thinking) Alibaba	Open-Source	1,073.26	41.50	2,586.2
13	Qwen3-30B-A3B-Thinking-2507 Alibaba	Open-Source	4,846.07	85.50	5,671.6
14	Qwen3-235B-A22B-Thinking-2507 Alibaba	Open-Source	5,927.84	92.00	6,443.3
15	Qwen3-32B (thinking) Alibaba	Open-Source	6,135.86	85.50	7,179.0
16	Qwen3-235B-A22B (thinking) Alibaba	Open-Source	6,545.30	85.00	7,700.4
17	gemini-3-pro-preview Google	Commercial	7,523.07	95.00	7,929.5
18	AReaL-boba-2-32B inclusionAI	Open-Source	6,901.34	85.00	8,119.2
19	Qwen3-30B-A3B (thinking) Alibaba	Open-Source	6,412.52	76.50	8,388.9
20	Qwen3-14B (thinking) Alibaba	Open-Source	6,850.90	77.00	8,897.3
21	AReal-boba-2-14B inclusionAI	Open-Source	7,519.10	79.50	9,461.4
22	AceReason-Nemotron-7B NVIDIA	Open-Source	7,082.74	67.50	10,419.6
23	AceReason-Nemotron-14B NVIDIA	Open-Source	8,515.95	76.50	11,128.7
24	gemini-2.5-flash Google	Commercial	9,884.73	85.00	11,629.1
25	gemini-2.5-pro Google	Commercial	9,808.19	79.00	12,417.9
26	AReal-boba-2-8B inclusionAI	Open-Source	10,521.25	70.50	14,959.2
27	Qwen3-8B (thinking) Alibaba	Open-Source	10,637.60	65.50	16,251.0
28	Qwen3-4B (thinking) Alibaba	Open-Source	13,639.89	58.00	23,517.1
30	gemini-2.5-flash-lite Google	Commercial	54,042.28	40.50	133,435.3

Benchmark Overview

OckBench provides comprehensive evaluation across multiple dimensions

Total Questions

400

Task Domains

2

Questions per Domain

200

Models Evaluated

24

Benchmark Composition

OckBench is structured to test LLMs' reasoning efficiency across two complementary domains: mathematical problem solving and coding skills. To better expose token-efficiency differences, we select questions that exhibit high variance in decoding token usage among baseline models.

Mathematics and Reasoning Tasks (200 questions): We adopt GSM8K, AIME24, and AIME25 as core reasoning benchmarks. We select the top 200 questions that exhibit high variance in decoding token usage among baseline models, ensuring the benchmark emphasizes efficiency contrast rather than merely ranking by accuracy.
Software Engineering Tasks (200 questions): For the coding domain, we build a lightweight variant of MBPP, supplemented by 200 carefully curated real-world coding problems. These coding tasks cover algorithmic challenges, code transformation, debugging, and small-scale project tasks.

Example Tasks

Sample problems from OckBench-Math and OckBench-Coding

These examples illustrate the types of problems where token efficiency varies significantly across models.

Math Problem (GSM8K)

Question: A store sells notebooks for $3 each. If you buy more than 10, you get a 20% discount on the total price. How much would it cost to buy 15 notebooks?

Domain: Mathematics | Source: GSM8K

Token variance: Some models use 200 tokens, others use 2,000+ for the same answer.

Math Problem (AIME)

Question: Find the number of ordered pairs (a,b) of integers such that a² + b² = 2024 and both a and b are positive.

Domain: Mathematics | Source: AIME 2024

Token variance: High variance across models due to different reasoning approaches.

Coding Problem (MBPP)

Task: Write a function to find the longest common subsequence of two strings. For example, lcs("ABCDGH", "AEDFHR") should return 3 (the LCS is "ADH").

Domain: Coding | Source: MBPP variant

Token variance: Efficient models write concise code with brief explanations.

Future Work: More Domains

Planned Extension: We plan to extend OckBench to additional domains such as algorithmic challenges, debugging tasks, and code transformation problems to provide more comprehensive token efficiency evaluation.

Status: Coming in next version | Focus: Broader coverage

Stay tuned for expanded benchmark coverage across more reasoning domains!

Key Findings

2× token variance among top models: Gemini-2.5 Pro used 2× more tokens than GPT-5 for similar accuracy (5,198 vs 2,336 tokens).
GPT-4o is most token-efficient: Best reasoning efficiency of 14.1 (math) and 12.9 (coding) despite lower accuracy.
"Thinking" modes costly: Qwen3-14B thinking used 2.7× more tokens than non-thinking (8,190 vs 3,010) without proportional gains.
Commercial models lead: 60.8% average accuracy vs 35.3% for open-source on math tasks.
10-18× efficiency differences: Models with comparable accuracy differ wildly in token consumption.
Size doesn't guarantee efficiency: Smaller models sometimes use more tokens than larger ones for the same tasks.

Citation

If you find OckBench useful for your research, please cite our work

@inproceedings{du2025ockbench,
  author    = {Du, Zheng and Kang, Hao and Zhu, Ligeng and Han, Song and Krishna, Tushar},
  title     = {OckBench: Tokens are Not to Be Multiplied without Necessity},
  booktitle = {NeurIPS 2025 Workshop on Efficient Reasoning},
  year      = {2025}
}